Læs-Tænk-Regn til mellemtrinnet
Hvad er Læs-Tænk-Regn
Læsning er ikke kun dansklærerens domæne mere, og i UVM’s “Læseplan for faget matematik” står der da også under det tværgående emne “Sproglig udvikling”:
“Det er centralt, at eleverne arbejder med, hvordan viden om fagteksters formål og struktur kan anvendes til udviklingen af læsestrategier. Dette gælder bl.a. hensigtsmæssige strategier til: Søgning, aflæsning og udvælgelse af relevant information fra såvel sammenhængende som ikkesammenhængende tekster.”
(UVM,2015)
Her hos Matematikfessor vil vi selvfølgelig gerne støtte op om udviklingen, og vi har derfor udarbejdet et koncept, der hedder Læs-Tænk-Regn (LTR). Du finder LTR-opgaverne på Matematikfessors Lærerværelse under genvejen “PDF-opgaver”.
Hensigten med LTR-opgaverne er, at eleverne skal udvikle deres kompetencer inden for faglig læsning af matematiske tekster ved at lære at benytte hensigtsmæssige læsestrategier samt at være aktive i læreprocessen.
Herudover vil vi også med LTR til mellemtrinnet tilgodese, at eleverne skal kunne (jf. Færdighedsmål efter 6. kl.):
- mundtligt og skriftligt kommunikere varieret med og om matematik.
- anvende fagord og begreber mundtligt og skriftligt.
Opgavernes opbygning
På mellemtrinnet (4.-6. klasse) består LTR af en række tekstopgaver, der hver afsluttes med et spørgsmål angivet i kursiv. Eleverne skal læse teksten (evt. med hjælp fra læreren), og målet er, at de selv skal kunne uddrage de nødvendige informationer for at kunne svare på det matematiske spørgsmål, der stilles. Der er selvfølgelig forskellige måder, hvorpå man kan stille regnestykket op i kladdehæfte.
Procesnotat
For nogle elever kan det være vanskeligt at uddrage opgavens problemstilling samt holde styr på en mængde andre informationer undervejs. Et procesnotat er en notatteknik, der kan hjælpe disse elever gennem tekststykkerne. Et procesnotat kan derudover også bruges i hele klassen som en måde, hvorpå man kan arbejde med overblikket over en matematisk tekst, samt udtrykke sig med ord omkring sin matematiske proces. Eleverne kan arbejde sammen eller i makkerpar om at udfylde procesnotatet.
Vi har udarbejdet to varianter af procesnotatet. Et simpelt procesnotat samt ét, der indeholder overslag og vurdering af overslaget .
For at udnytte procesnotatets potentiale er det vigtigt, at eleverne bruger ord til at beskrive processerne. Det er selvfølgelig altid lærerens professionelle vurdering, om procesnotatet egner sig til en given matematisk tekst. Det bør aldrig i sig selv være et mål at udfylde procesnotatet, og eleverne bør ikke bruge det hver eneste gang, de skal løse en LTR – det vil blive for omfattende og tidskrævende. Pointen er, at eleverne internaliserer procesnotatets fremgangsmåde (eller dele heraf), så de af sig selv vil kunne skabe et overblik over en given matematisk tekst og benytte den fremgangsmåde, der er relevant. Man kan vælge at bruge procesnotatet i arbejdet med LTR, men det kan også bruges i andre sammenhænge med andre matematiske tekster.
| Problem (Hvad er spørgsmålet) |
Hvor meget skal Fessor betale for hele sit indkøb? |
| Oplysninger (Hvad ved jeg i forvejen) |
Der er en skoletaske til 499 kr. En lineal 32 kr. Farveblyanter til 20 kr. 5 blyanter á 3 kr. 2 mapper á 6 kr. En blyantspidser til 15 kr. |
| Tegning |  |
| Løsningsstrategi (Hvad gør jeg) |
Jeg starter med at regne ud, hvor meget jeg skal betale for blyanter og mapper. 5 gange 3 og 2 gange 6. Og så plusser jeg det med alle de andre tal. |
| Udregning | 5 · 3 = 15 2 · 6 = 12 499 + 32 + 20 + 15 + 12 + 15 = 593 kr. |
| Resultat (Skrives med et ord) |
Fessor skal betale 593 kr for hele sit indkøb. |
Matematik-ordbog
Matematik-ordbogen er tiltænkt elever på mellemtrinnet og i udskolingen. Udgangspunktet for matematik-ordbogen er opbygning af ordforråd inden for matematiske fagudtryk, begreber og symboler. I UVM’s læseplan for faget matematik (under det tværgående emne “Sproglig udvikling”) er området beskrevet således:
“I matematik er det vigtigt, at eleverne udvikler et præcist fagsprog og lærer centrale fagord og begreber i faget, f.eks. addition, radius og areal. Undervisningen skal have fokus på, at eleverne skal kunne adskille hverdagssprog fra fag sprog, herunder fokus på førfaglige ord og hverdagsbegreber, som har en specifik betydning i matematik f.eks. forhold, sider og at skære. Eleverne skal også arbejde med ordforståelsesstrategier til selvstændig tilegnelse af nye fagord og begreber, udnyttelse af konteksten til forståelse af ord samt opslag i analoge og digitale opslagsværker.
(UVM,2o15)
Vedrørende opbygning af ordforråd inden for matematiske fagudtryk, begreber og symboler har vi valgt at understøtte tilegnelsen i form af arbejde med en matematik-ordbog. Ordbogen findes som print på FessorsForum, hvor du også har fundet denne folder. I kan vælge at lave én fælles matematik-ordbog i klassen som I hænger op, eller at eleverne laver hver deres egen. Matematik-ordbogen kan både bruges som før- og efterlæsningsstrategi.
I matematik-ordbogen bearbejdes 4 forskellige typer ord/begreber/symboler. Det er vigtigt, at du som lærer skelner mellem de forskellige.
- Ord, der peger på regnearter (f.eks “tilsammen”, “tilbage”, “dele” osv.)
- Hverdagsord der optræder som matematikord (f.eks “bestem”, “skære”, “side” osv.)
- Særlige fagord og begreber (f.eks. “tabel”, “retvinklet”, “mellemregning” osv.)
- Matematiske symboler (f.eks. cm2, %, > osv.)
Siderne i ordbogen er enkeltsider, og I kan derfor sammensætte jeres ordbog, så den passer til netop jeres klasse. På mellemtrinnet vil der kunne arbejdes med alle fire sider, mens udskolingen kan få gavn af at fokusere på “Særlige fagord og begreber” samt “Matematiske symboler”.
I kan vælge at lave én fælles matematik-ordbog i klassen som I hænger op, eller at eleverne laver hver deres egen. Matematik-ordbogen kan både bruges som før- og efterlæsningsstrategi.
Nedenfor kan du se, hvordan matematik-ordbogens delelementer ser ud. Vi har givet flere eksempler til dig som lærer, hvor eleverne kun får ét eksempel på udfyldning.
Ord der pege på regnearter
| Plus | Minus |
|---|---|
| Tilsammen | Tilbage |
| I alt | Forskellen/differensen |
| Den samlede pris | Hvor meget mere |
| Omkreds | Imellem |
| Lægge sammen | Trække fra |
| Gange | Dividere |
| Areal | Dele |
| Et beløb/tal, der skal tages et bestemt antal gange | Hver |
| Rumfang | Frekvens |
| Kombinationer | Forhold mellem tal |
| Valgmuligheder | Brøker |
| Omsætning | En mindre mængde ud af en stor mængde |
| Procent | Omsætning |
| Procent |
Hverdagsord der optræder som matematikord
| Ord | Hverdags-betydning | Matematik-betydning |
|---|---|---|
| Sildeben | Et slags fiskeskelet. | En figur man bruger, når man skal finde punkter, der bagefter kan tegne ind i et koordinatsystem. |
| Bestem | Når nogen bestemmer f.eks. i en leg. | Bestem betyder at regne sig frem til noget. |
| Kurve | Beholdere til at have noget i. | En linje, der består af punkter. En “hakket linje”. |
| Ret | Noget mad. Når nogen har ret i hvad de siger. | Betyder lige |
Særlige fagord og begreber
| Symbol | Hvad betyder det? | Tegn el. skriv en opgave eller forklaring til ordet |
|---|---|---|
| Diameter | En lige linje, der går fra kant til kant gennem en cirkels centrum. |  |
| Rumfang | Størrelsen af et rum inde i f.eks. en kasse. Formlen er l · b · h Svaret skal være noget med kubik. |
Kassen er 8 cm · 2 cm · 10 cm = 160 cm3 |
| Sum | Når man lægger tal sammen. | Hvad er summen af 8,6og 2? 8+6+2 = 16 Svar = 16 |
| Brøkdel | Når man tager en del af noget. Når nogen har ret i hvad de siger. | En 4. del af 100 skrives sådan: ¼ af 100 = 25 |
Særlige fagord og begreber
| Symbol | Hvad hedder det? | Hvordan bruges det? |
|---|---|---|
| cm2 | Kvadratcentimeter | Det kan bruges når man skal skrive et areal af noget. |
| % | Procent | Det betyder hundrededel. Man kan f.eks. bruge det, når man skal regne rabat. |
| > | Større end | Når man skal finde et resultat. der kan f.eks. stå X > 23. Så ved man at resultatet er større end 23. |
| () | Parenteser | Man skal huske at regne det i parentesen først. |
Hvordan kan du bruge Læs-Tænk-Regn
I LTR-opgaverne er det essentielt, at eleverne forstår teksten, før de kan omsætte den til et regnestykke. Matematikfessor foreslår derfor denne fremgangsmåde ved brug af LTR-opgaverne:
1. Forberedelse
Læs opgaven og facitarket og tag stilling til, om et eller flere ord skal bearbejdes i matematik-ordbogen. Tag også stilling til om eleverne skal arbejde alene, i par eller i grupper. Overvej om alle eller dele af klassen kan have gavn af at arbejde med et procesnotat.
2. Før-læsning
- Hvis I bruger matematik-ordbogen som før-læsningsaktivitet kan du på forhånd have plukket relevante ord ud, som I kan skrive i ordbogen, inden i begynder selve arbejdet med opgaven. Dette skærper elevernes opmærksomhed omkring det matematiske sprog, samt aktiverer og bygger videre på elevernes forforståelse.
- Præsentér for eleverne på hvilken måde du gerne vil have, at de skal stille regnestykkerne op, eller om du ønsker, at de kun arbejder i procesnotatet.
- Som en før-læsnings aktivitet kan I desuden bruge de lektioner (forklarings-videoer), der ligger tilgængeligt på Matematikfessor.dk. De ligger der, hvor du downloader LTR-opgaverne. Hvis du vil sikre dig, at eleverne kan regnemetoden, der bliver brugt i en given LTR-opgave kan du give lektionen (forklarings-videoen) for, og de kan efterfølgende teste sig selv i Test-Dig-Selv – 5 skarpe. Du kan også give opgavesæt for, der omhandler samme matematiske emner som de LTR-opgaver, I skal arbejde med.
3. Under-læsning
Eleverne læser opgaven, tænker, og skriver regnestykkerne ned i kladdehæftet eller i procesnotatet. De kan arbejde alene, eller i grupper, hvor de kan udveksle idéer og valg af regnemetode, samt træne evnen til at udtrykke sig mundtligt omkring matematikken. Nedenfor kommer forslag til arbejdsmetoder:
3a.) Cooperative Learning variationer
- Chef-sekretær Elevernearbejder i par. Den ene påtager sig stillingen som chef, den anden som sekretær. Sekretæren starter med at læse teksten højt. Chefen forklarer derefter hvordan opgaven skal løses (men uden at skrive ned).
- Team-par-soloTeam: Eleverne er 4 personer i et team. De får lidt tid til at arbejde sammen om at løse den første opgave. Læreren giver herefter løsningen og forklarer udregningen. Hvis opgaven er løst korrekt går eleverne til par-arbejde. Hvis ikke, løser de også næste opgave som team.
Par: Team-medlemmerne danner to par inden for teamet og løser næste opgave i par. Hvis det lykkes at løse opgaven, går de over til solo. Hvis ikke, går de tilbage til at arbejde i teamet.
Solo: Hver elev løser næste opgave alene. Hvis det ikke lykkes, går de tilbage til pararbejde.
3b. Læse-løb
- Forberedelse: Ca. 10 tekststykker fra Læs-Tænk-Regn klippes ud, nummereres og hænges op rundt omkring i klassen, på gangen eller i et fællesrum. Tekststykkerne må gerne gemmes lidt væk f.eks under et bord, tæt på gulvet eller højt oppe på væggen så eleverne skal lede efter dem. Eleverne inddeles nu i par og bedes medbringe et stykke papir, en blyant og et viskelæder.Aktiviteten: Nu sendes eleverne på jagt. Når eleverne finder en opgave, skal de skrive nummeret på opgaven på deres papir, læse opgaven, løse den og skrive facit ud for opgavenummeret. De går herefter på jagt efter en ny opgave. Så- dan fortsættes indtil de har løst alle opgaverne. Når eleverne er færdige går de i klassen, hvor I gennemgår opgaverne i plenum.Differentiering: Du kan hænge nogle ekstra LTR tekststykker op fra en anden LTR, evt. i en anden farve, til de hurtige elever. Du kan blande tekststykker fra forskellige klassetrin og derved differentiere niveauet
4. Efter læsning
Efterlæsnings-aktiviteter kan tage mange andre former end den traditionelle klassegennemgang. Her kommer 4 bud på efterbehandling af LTR-opgaverne:
4a) Kend dit fagord
Eleverne arbejder i par. Elev A trækker et af dagens fagord fra en bunke, og læser det højt for elev B. Eleverne finder sammen ud af hvilken en side det skal stå på i ordbogen (er det: “ord, der peger på regnearter”, “hverdagsord der optræder som matematikord”, “særligt fagord eller begreb” eller “matematisk symbol”). Elev B forklarer, hvad der skal skrives i de forskellige felter. Begge skriver ned.
4b) Film en forklaring
Eleverne tager udgangspunkt i en bestemt regneart eller en bestemt LTR-opgave, og skal nu omsætte den til en forklarings-video. Man kan vise dem i klassen, eller for en yngre klasse som introduktion til et emne. De kan også gemmes, hvis klassen har et fælles drev, så de kan bruge videoerne som opslagsværk.
4c) Lav en tegneserie
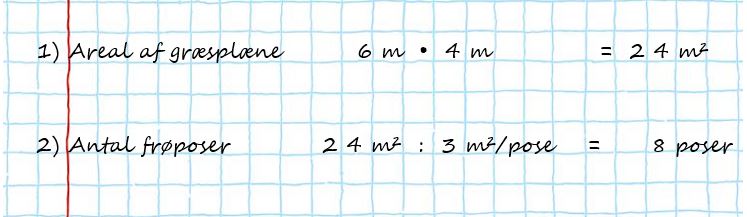
Lad eleverne omsætte LTR-opgaverne til en lille tegneserie. Et krav til opgaven kan være, at eleverne skal sørge for at have resultaterne på de forskellige stykker med i illustrationerne. Hvis resultatet af en opgave f.eks. viser, at Fessor skal købe 8 frøposer for at dække sin græsplæne, så skal det selvfølgelig illustreres i tegneserien. Du kan også lade eleverne lave deres egen LTR-opgave først, f.eks med 3 spørgsmål, der herefter skal illustreres i en tegneserie.
4d) Regnehistorier Eleverne
kan eventuelt producere deres egne regnehistorier (altså tekstbaserede matematikstykker) med facit. Her er det sproglige niveau og stavning ikke så vigtigt. Nogle af historierne kan læses op i klassen, som I fællesskab kan nå frem til en regnemetode. I kan derudover sætte hele klassens regnehistorier sammen til en bog.
Den passive elev
Hvis (eller rettere når) du støder på en elev, der spørger “hvad skal man i den her opgave” er det ikke altid det hjælper, at læse teksten én gang til. Eleven kan må- ske godt læse teksten højt, men aner ikke hvad han/hun skal stille op derefter. Da formålet med LTR er, at eleverne skal udvikle kompetencer inden for faglig læsning af matematiske tekster, bliver de nødt til at arbejde med at benytte hensigtsmæssige strategier og være aktive i læreprocessen. Du skal derfor ikke blot omformulere opgaven for eleven, men gå i dialog om opgaven med spørgsmål som: “Prøv at fortælle med dine egne ord, hvad der står.” “Hvor står spørgsmålet henne?” “Hvad får du at vide?” “Hvad kan du tegne til denne opgave?” Når eleven bruger sine egne ord til at formulere sig, har han/hun mulighed for at danne indre billeder af problemstillingen og dernæst vælge en løsningsstrategi, der er hensigtsmæssig.
- Hvad er Læs-Tænk-Regn
- Opgavernes opbygning
- Procesnotat
- Matematik-ordbog
- Ord der pege på regnearter
- Hverdagsord der optræder som matematikord
- Hvordan kan du bruge Læs-Tænk-Regn
- Den passive elev