Hensigten med LTR-opgaverne er, at eleverne skal udvikle deres kompetencer inden for faglig læsning af matematiske tekster ved at lære at benytte hensigtsmæssige læsestrategier samt at være aktive i læreprocessen.

Herudover vil vi også med LTR til indskolingen tilgodese, at eleverne skal kunne (jf. Færdighedsmål efter 3. kl.): Vise deres matematiske tænkning med uformelle skriftlige noter og tegninger, anvende enkle fagord og begreber mundtligt samt skriftligt.

Opgavernes opbygning

I indskolingen (1.-3. klasse) består LTR af en række små tekststykker, der hver afsluttes med et spørgsmål angivet i kursiv. Tekststykkerne er udformet som berettende tekster, fordi vi har valgt en teksttype, som eleverne allerede er fortrolige med i indskolingen. Til højre for tekststykket er en notatboks. Eleverne skal (evt. med hjælp fra læreren) læse teksten, og målet er, at de selv skal kunne uddrage de nødvendige informationer for at kunne svare på det matematiske spørgsmål, der stilles. Derefter skal eleverne bruge notatboksen, her er det op til dig som lærer, om du vil stille krav til, hvordan de skal udfylde den. Eleverne kan f.eks. tegne opgaven, de kan skrive regnestykket, eller de kan skrive resultatet. Her kan du som lærer differentiere i forhold til de forskellige elevers niveau.

Som noget nyt foreligger de nye LTR-opgaver til 1. og 2. klasse i to eksemplarer: Et med understøttende illustrationer og et uden (Se figur 1.). Læreren kan derved udlevere de illustrerede opgaver til de elever, der har svært ved at læse. Hvis nogle elever har brug for ekstra udfordring og har nemt ved at læse, kan man med fordel give dem nogle af de ældre LTR-opgaver, hvor sproget er sværere.

Vi har desuden ført Læs-Tænk-Regn helt ned i 0. klasse. Det har vi gjort, så du som lærer allerede i 0. klasse kan begynde tekstarbejdet med de elever, der er klar til dette.
Teksten i opgaverne er umiddelbart den samme i hvert spørgsmål, så elever, der endnu ikke kan afkode ordene bogstav-for-bogstav, derimod kan lære at genkende de enkelte ord som ordbilleder. De får derved en følelse af at kunne læse og at kunne løse matematikopgaver med tekst i. (Se figur 2)

Læsning i LTR

Vi har i de nyeste LTR-opgaver benyttet et lettere tilgængeligt sprog, så eleverne ikke skal bruge unødig energi på at afkode ordene, men i stedet kan koncentrere sig om matematikken. På de helt små klassetrin har vi tilpasset teksterne ved at bruge et forholdsvist stort antal lydrette ord og gentagelser. Herudover svarer lixtallet til, hvad man kan forvente af elever på det givne klassetrin. Tekststørrelse og periodelængde (antal ord mellem to punktummer) er også tilpasset klassetrinene.

Vi har i de nye LTR-opgaver desuden lettet læseforståelsen. Vi inddrager eksempelvis elevernes viden om verden ved at lade Fessor bevæge sig i forskellige kontekster, eleverne kender f.eks. “Fessor holder fødselsdag”. Eleverne kan bruge deres forforståelse samt ordforråd inden for emnet “fødselsdag” til lettere at genkende et ord som “lagkage”. De behøver derfor ikke at gå i stå i afkodningen.

I UVM’s læseplan for faget matematik står der under det tværgående emne “Sproglig udvikling” vedrørende ordkendskab, at:

”I matematik er det vigtigt, at eleverne udvikler et præcist fagsprog og lærer centrale fagord og begreber i faget, f.eks. addition, radius og areal. Undervisningen skal have fokus på, at eleverne skal kunne adskille hverdagssprog fra fagsprog, herunder fokus på førfaglige ord og hverdagsbegreber, som har en specifik betydning i matematik f.eks. forhold, sider og at skære. Eleverne skal også arbejde med ordforståelsesstrategier til selvstændig tilegnelse af nye fagord og begreber, udnyttelse af konteksten til forståelse af ord samt opslag i analoge og digitale opslagsværker. ”

(UVM, 2015)

Vedrørende opbygning af ordforråd inden for matematiske fagudtryk, begreber og symboler har vi valgt at understøtte tilegnelsen i form af arbejde med ordkendskabskort. Ordkendskabskortet ses som et eksempel på facitarket til den givne LTR-opgave og findes samtidig som skabelon til print på FessorsForum, hvor du har fundet denne folder.

På de små klassetrin består ordkendskabskortet af en model, hvor feltet i midten udfyldes med det ord/begreb, der skal arbejdes med. Herudover er der 3 andre felter, der skal udfyldes med:

En afklaring af ordets betydning.
En illustration (hvis muligt).
Udnyttelse af ordet i en matematisk kontekst.

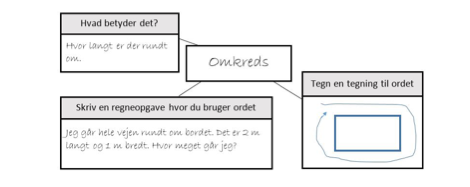
På facitarket til de nye LTR-opgaver har vi listet fagudtryk og andre særlige ord. Det er vigtigt at skelne imellem ord, der kan være svære at afkode, og ord som har en særlig signifikans i forhold til, at eleverne udvikler et egentligt fagsprog. Her er det vigtigt som lærer kun at udvælge og bearbejde de ord, som du finder relevante i et ordkendskabskort. Et ord som “muffin” kan være svært for en 2.klasseselev at læse, men er ikke nødvendigvis et ord, der er relevant at bruge krudt på i forhold til f.eks. et ord som “firkantet”.
I de små klasser kan du som lærer vælge at aftegne ordkendskabskortet på tavlen/smartboardet og udfylde det sammen med eleverne. Du kan også finde den printvenlige version af ordkendskabskortet på FessorsForum og lave den som A3 til ophæng i klassen.

Som progression kan man på mellemtrinnet og i udskolingen overveje, at lade eleverne udfylde ordkendskabskortet på egen hånd eller i grupper. En anden variation er ikke på forhånd at udpege de relevante ord. Det er vigtigt at pointere, at det ikke bør være et mål i sig selv at udfylde ordkendskabskort! Ordkendskabskort er tiltænkt som en før-læsningsstrategi, der skærper opmærksomheden omkring det matematiske sprog, samt aktiverer og bygger videre på elevernes forforståelse.

Guide til LTR – sådan bruger du LTR-opgaverne

I LTR-opgaverne er det essentielt, at eleverne forstår teksten før, at de kan omsætte den til et regnestykke. Eleverne kan godt se, at der står nogle tal inde i teksten, men hvad der skal gøres med disse tal kan være svært at overskue.
MatematikFessor foreslår derfor denne fremgangsmåde ved brug af LTR-opgaverne:

1) Forberedelse

Læs opgaven og facitarket og tag stilling til om et eller flere ord skal bearbejdes i et ordkendskabskort. Tag også stilling til om eleverne skal arbejde alene, i par eller i grupper.

2) Før-læsning

Tal med eleverne om konteksten: Fortæl eleverne hvor Fessor nu er henne. Hvad ved de f.eks. om Zoo? Gør det kort, og gør det for at aktivere deres forforståelse.
Gennemgå relevante ord. Er der nogle ord, der skal arbejdes med i et ordkendskabskort? Er der nogle ord, der kan være svære at læse?
Forslag til udfyldelse af notatboks: Hvis det er første gang, I arbejder med LTR, kan du spørge eleverne, hvordan de forestiller sig, at man kan udfylde notatboksen.
Som en før-læsnings aktivitet kan I desuden bruge de lektioner (forklarings-videoer), der ligger tilgængeligt på MatematikFessor.dk. De ligger der, hvor du downloader LTR-opgaverne. Hvis du vil sikre dig, at eleverne kan regnemetoden, der bliver brugt i en given LTR-opgave, kan du give lektionen (forklarings-videoen) for, og de kan efterfølgende teste sig selv i Test-Dig-Selv – 5 skarpe. Du kan også give opgavesæt for, der omhandler samme matematiske emner som de LTR-opgaver, I skal arbejde med.

3) Under-læsning

Eleverne læser opgaven, tænker og skriver eller tegner i notatboksen. De kan arbejde alene, eller i grupper, hvor de kan udveksle idéer og valg af regnemetode, samt træne evnen til at udtrykke sig mundtligt omkring matematikken. Nedenfor kommer forslag til arbejdsmetoder:

3a) Cooperative Learning variationer

Chef-sekretær
Eleverne arbejder i par. Den ene påtager sig stillingen som chef, den anden som sekretær. Sekretæren starter med at læse teksten højt. Chefen forklarer derefter, hvordan opgaven skal løses (men uden at skrive ned). Sekretæren udfører notatarbejdet og evt. selve udregningen. Hvis chefen giver instruktioner, der fører til løsning af opgaven, roser sekretæren ham/hende. Ellers hjælper sekretæren med at få løst opgaven, og roser dernæst chefen. Herefter bytter de roller.

Rollelæsning
Eleverne er sammen 3 og 3. Elev A læser opgaven. Alle 3 taler om, hvordan de kan løse opgaven. Elev B tegner. Elev C skriver regnestykket og resultatet. Herefter bytter de roller.

Mix og match
Når eleverne har lavet opgaven, kan man klippe siden over i små dele, så der er lapper med tekststykker og lapper med (udfyldte) notatbokse. Sørg for, at der i klassen er en seddel til hver elev, hvor sedlerne passer sammen 2 og 2. Læreren siger “Mix”, og eleverne går rundt mellem hinanden og bytter kort med dem de møder undervejs. Hver elev må kun have et kort ad gangen. Når læreren siger “Match” leder eleverne efter den klassekammerat, der har det kort, der matcher deres. Altså skal de finde et tekststykke, der passer til deres notatboks. Når alle har fundet deres match og tjekker kortene, siger læreren “Mix”, og legen starter forfra.

3b) Læse-løb

Forberedelse:
Ca. 10 tekststykker fra Læs-Tænk-Regn klippes ud, nummereres og hænges op rundt omkring i klassen, på gangen eller i et fællesrum. Tekststykkerne må gerne gemmes lidt væk f.eks. under et bord, tæt på gulvet eller højt oppe på væggen, så eleverne skal lede efter dem. Eleverne inddeles nu i par og bedes medbringe et stykke papir, en blyant og et viskelæder.

Aktiviteten:
Nu sendes eleverne på jagt. Når eleverne finder en opgave, skal de skrive nummeret på opgaven på deres papir, læse opgaven, løse den og skrive facit ud for opgavenummeret. De går herefter på jagt efter en ny opgave. Sådan fortsættes indtil de har løst alle opgaverne. Når eleverne er færdige går de i klassen, hvor I gennemgår opgaverne i plenum.

Differentiering:
Du kan hænge nogle ekstra LTR-tekststykker op fra en anden LTR, evt. i en anden farve, til de hurtige elever.
Du kan blande tekststykker fra forskellige klassetrin og derved differentiere niveauet.

4) Efter-læsning

Eventuel klassegennemgang: Et par elever kan vise, hvordan de har tegnet/skrevet.
Videre arbejde: Eleverne kan eventuelt producere deres egne regnehistorier (altså tekstbaserede matematikstykker) med facit. Her er det sproglige niveau og stavning ikke så vigtigt. Nogle af historierne kan læses op i klassen, som i fællesskab kan nå frem til en regnemetode. I kan derudover sætte hele klassens regnehistorier sammen til en bog.

Den passive elev

Hvis (eller rettere når) du støder på en elev, der spørger “hvad skal man i den her opgave”, er det ikke altid, det hjælper, at læse teksten én gang til. Eleven kan måske godt læse teksten højt, men aner ikke hvad han/hun skal stille op derefter. Da formålet med LTR er, at eleverne skal udvikle kompetencer inden for faglig læsning af matematiske tekster, bliver de nødt til at arbejde med at benytte hensigtsmæssige strategier og være aktive i læreprocessen. Du skal derfor ikke blot omformulere opgaven for eleven, men gå i dialog om opgaven med spørgsmål som: “Prøv at fortælle med dine egne ord, hvad der står.” “Hvor står spørgsmålet henne?” “Hvad får du at vide?” “Hvad kan du tegne til denne opgave?”. Når eleven bruger sine egne ord til at formulere sig, har han/hun mulighed for at danne indre billeder af problemstillingen og dernæst vælge en løsningsstrategi, der er hensigtsmæssig.